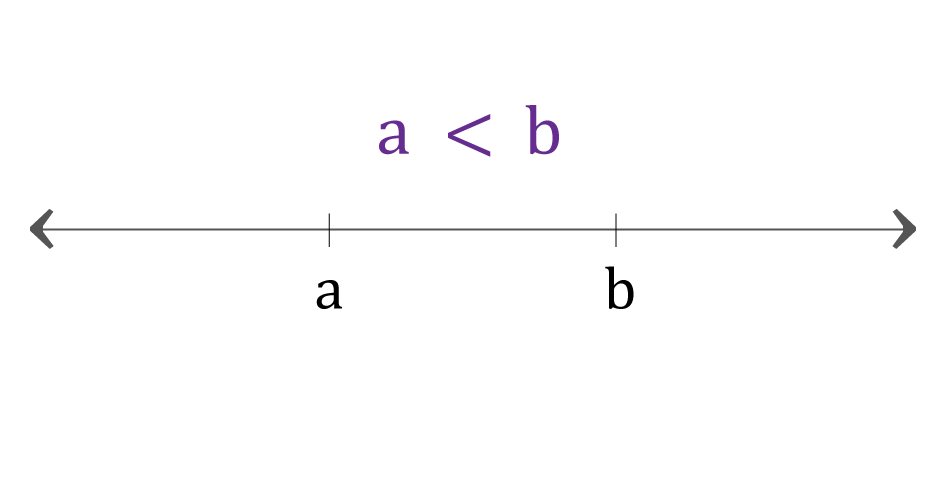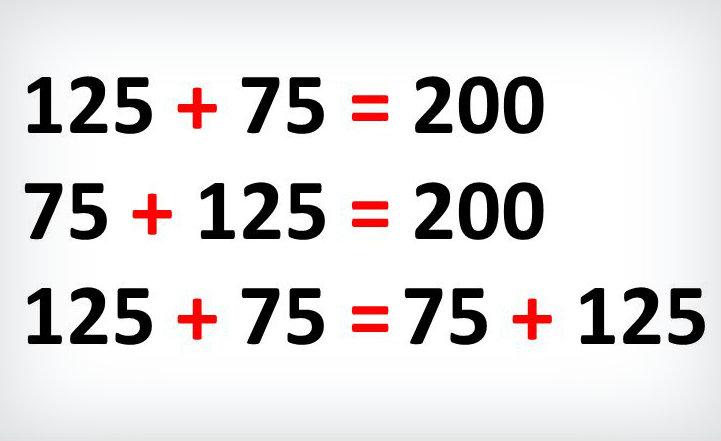LOS NÚMEROS ENTEROS
Los números naturales no alcanzan a abarcar las situaciones reales de la vida. Por ejemplo: ¿Cuanto dinero tendrías en total si solo dispones de $100 pesos y debes $150?
Los
números enteros son una ampliación de los naturales:
Los números enteros pueden ser:
• Enteros positivos (se escriben con el signo +)
• Enteros
negativos (se escriben con el signo -)
• El cero es un entero neutro.
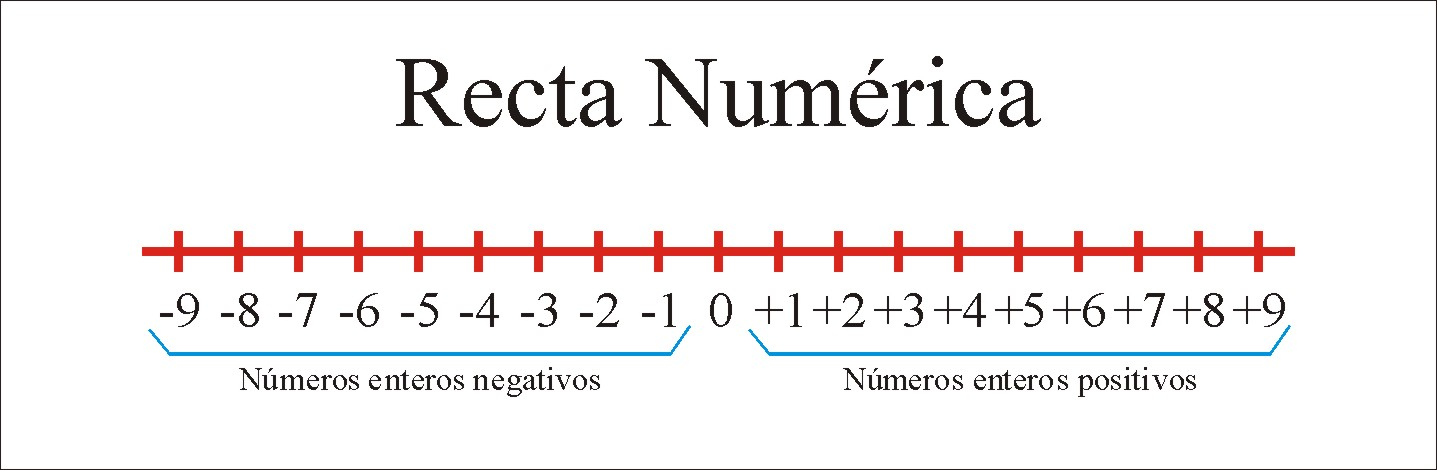
LA RECTA NUMÉRICA
Los números enteros se pueden representar en una recta numérica, en donde el cero va en la mitad, a la izquierda de este los enteros negativos y a la derecha los enteros positivos.
Ordenar
y comparar números enteros
Cuanto
más a la derecha esté un número situado en la recta numérica mayor es. Cuanto
más a la izquierda esté situado menor es.
Enteros positivos
Enteros negativos
Valor
absoluto
En
matemáticas, el valor absoluto o módulo de un número real es su valor numérico
sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por
ejemplo, 3 es el valor absoluto de +3 y de -3.
Opuesto de un número entero
El
opuesto de un número es el número que al ser sumado con él da de resultado el
número 0. El opuesto de un número tiene el mismo valor absoluto, pero signo
contrario.
Se escribe así:
Op(+a) = -a
Op(-a) = +a
SUMA Y DIFERENCIA DE ENTEROS
Suma
En la
suma de dos números enteros, se determina por separado el signo y el valor
absoluto del resultado. Se debe tener en
cuenta lo siguiente:
- * Si
ambos sumandos tienen el mismo signo: ese es también el signo del resultado, y
su valor absoluto es la suma de los valores absolutos de los sumandos.
- * Si
ambos sumandos tienen distinto signo:
El
signo del resultado es el signo del sumando con mayor valor absoluto.
El
valor absoluto del resultado es la diferencia entre el mayor valor absoluto y
el menor valor absoluto, de entre los dos sumandos.
Ejemplos
(+21) +
(−13) = +8
(+17) +
(+26) = +43
(−41) +
(+19) = −22
(−33) +
(−28) = −61
Resta
Resta
Es
la operación contraria a la suma. Los términos de la resta se llaman minuendo y
substraendo, el resultado se llama diferencia. El minuendo es el número
primero, es el número al que le restan.
El signo del resultado es el signo del sumando con mayor valor absoluto.
Expresiones
sencillas con paréntesis. El signo más (+) puede indicar suma o que el número
es positivo. El signo menos (-) puede indicar resta o que el nº es negativo. No
podemos escribir dos signos seguidos, debemos separarlos mediante un paréntesis.
+(+a)
= +a
-(-a)
= +a
+(-a)
= -a
-(+a)
= -a
Si
los dos signos son iguales el resultado es positivo y si los dos signos son
distintos el resultado es negativo
Suma y diferencia de
enteros con paréntesis.
Cuando se presenten ejercicios del tipo:
• (-5) + (-2) = -5 – 2 = - 7
• (+3) - (-7) = 3 + 7 = 10
Deberemos
1º) Eliminar los paréntesis
2º) Operar adecuadamente los números resultantes
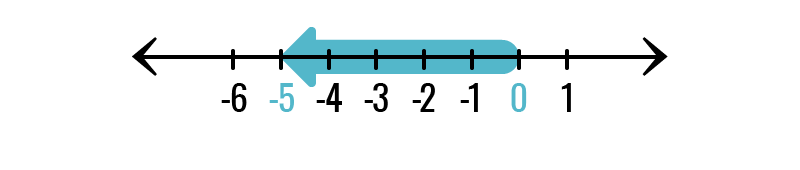
Suma y resta de enteros representada en recta numérica
Propiedad
conmutativa
Es
la propiedad que nos muestra que el resultado de la suma o la multiplicación no
depende del orden. Esto quiere decir que podemos sumar o multiplicar los
números en el orden que queramos.
Propiedad
asociativa
Esta
propiedad dice que la suma o multiplicación de varios números enteros no
depende de la forma en que se asocien.
Propiedad
idéntica o reflexiva
Establece que toda cantidad o expresión es igual a sí
misma.
Ejemplos:
2a
= 2a; 7 + 8 = 7 + 8; x = x
Propiedad
simétrica
Consiste en poder cambiar el orden de los miembros sin que la
igualdad se altere.
Ejemplos:
Si
39 + 11 = 50, entonces 50 = 39 + 11
Si
a - b = c, entonces c = a - b
Si
x = y, entonces y = x
Propiedad
transitiva
Enuncia que si dos igualdades tienen un miembro en común, los otros
dos miembros también son iguales.
Ejemplos:
Si 4
+ 6 = 10 y 5 + 5 = 10, entonces 4 + 6 = 5 + 5
Si x
+ y = z y a + b = z, entonces x + y = a + b
Si m
= n y n = p, entonces m = p
Producto
y división de enteros
Producto
de enteros
Para
multiplicar enteros debemos:
1º)
Multiplicar los números sin signo
2º)
Aplicar la regla de los signos
División
de enteros
Para
dividir enteros debemos:
1º)
Dividir los números sin signo
2º)
Aplicar la regla de los signos
EJERCICIOS PARA REFORZAR ASIGNATURA
Imprime y realiza las actividades a continuación. Una vez realizadas, entrega con excelente presentación al docente del área, para su posterior sustentación. Fecha de entrega: semana del 22 al 26 de abril.
Imprime y realiza las actividades a continuación. Una vez realizadas, entrega con excelente presentación al docente del área, para su posterior sustentación. Fecha de entrega: semana del 22 al 26 de abril.
Información obtenida de