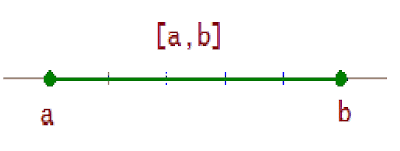PORCENTAJES
Debemos
de partir del significado de la palabra. Si separamos la primera parte de la
palabra, tendremos por centaje (por – ciento) – una medida con base 100, o sea,
es lo mismo que dividir un número por 100.
Un
porcentaje se puede estudiar como una razón: es una fracción con denominador
100.
Un 16 por ciento (16 %), es la
razón 16 / 100
Ejemplo
El
16 % de 1200 = la fracción 16 / 100 de 1200 = 0,16 · 1200 = 0,16
· 1200 = 192.
*
Un porcentaje puede calcularse multiplicando por el número decimal asociado.
El número decimal
asociado al 16 % es 16 / 100 = 0,16. Por tanto, para hallar el 16 % de
cualquier cantidad se multiplicará esa cantidad por 0,16. Así 16 % de 1200 =
1200 · 0,16 = 192.
Los porcentajes son partes por cada cien. Entonces, ¿cómo
funciona esto para porcentajes mayores que 100% como 109%?
Video El significado de 109%
Calcular porcentajes mentalmente
Para hallar el 45% de alguna
cantidad, primero se determina el 10%, luego se multiplica el resultado por 4 y
por último se suma la mitad del primer resultado.
Ejemplo
Determina el 45% de 80.
1. 80 /
10 = 8
2.
8 x 4 = 32
3.
8 / 2 = 4
4.
32 + 4 = 36
ACTIVIDADES PARA PRACTICAR
2. Porcentajes
INTERVALO
Un
intervalo es un espacio métrico comprendido entre dos valores. Específicamente,
un intervalo real es una parte de recta entre dos valores dados, un conjunto
medible y tiene la misma cardinalidad de la recta real.
Notación.
Existen dos notaciones principales: en un caso se utilizan corchetes y
corchetes invertidos; en el otro, corchetes y paréntesis.
Intervalo abierto. (a, b) o bien ]a, b[. Es
el conjunto de todos los números reales mayores que a y menores que b. No
incluye los extremos.
(a , b ) = {x ϵ R / a < x <
b }
Intervalo cerrado. Intervalo cerrado, [a, b], es
el conjunto de todos los números reales mayores o iguales que a y menores o iguales
que b. Sí incluye los extremos.
[a , b ] = {x ϵ R / a ≤ x ≤ b }
Intervalo semiabierto
por la izquierda. (a, b], es el conjunto de todos los números
reales mayores que a y menores o iguales que b.
Intervalo
semiabierto por la derecha. [ a, b), es
el conjunto de todos los números reales mayores o iguales que a y menores que b.
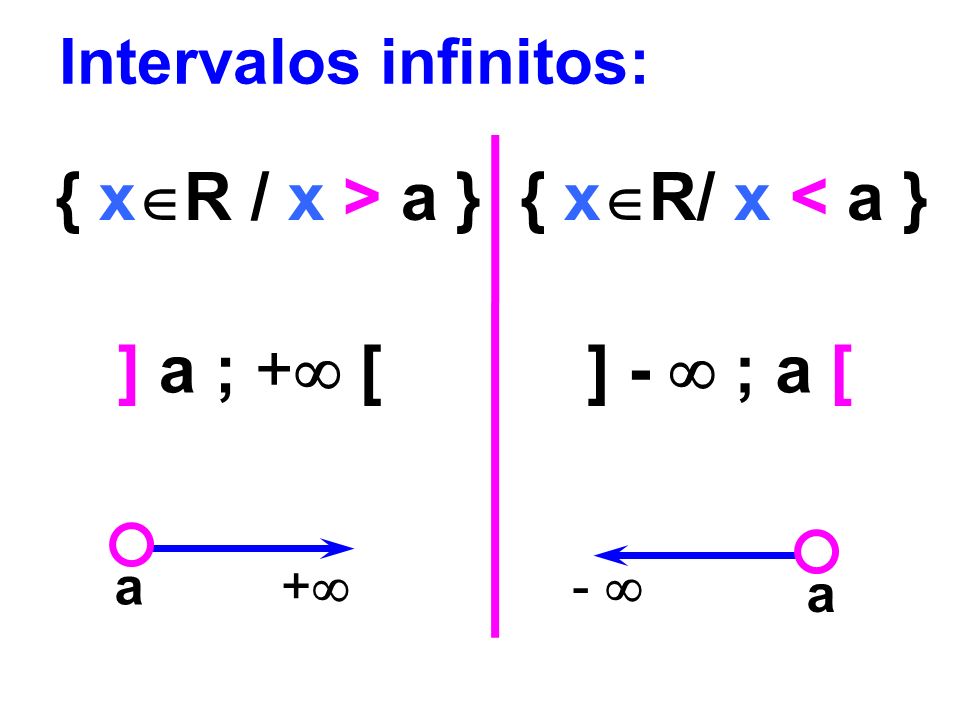
Intervalo infinito.
Incluye un extremo e infinito por la derecha. Con la notación [a, ∞) indicamos.
ACTIVIDADES PARA PRACTICAR
ACTIVIDADES PARA REFORZAR
Imprime y realiza las actividades a continuación. Una vez realizadas, entrega con excelente presentación al docente del área, para su posterior sustentación. Plazo de entrega: semana del 22 al 26 de abril.
Información
obtenida de